Light travels in a straight line. When light is reflected by a mirror, the incoming angle is equal to the reflection angle. When light enters water, it changes its directions according to Snell’s law. …
Or does it?
These light behaviors are not as intuitive as we think if we really want to explain them in quantum mechanics. We have to keep in mind, when a light particle – photon – travels from point A to point B, the photon takes all paths available in the universe! Correct, not just the straight line between A and B, but also any weird curves you can imagine starting from A to B.

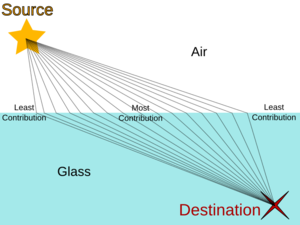
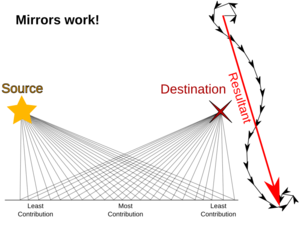
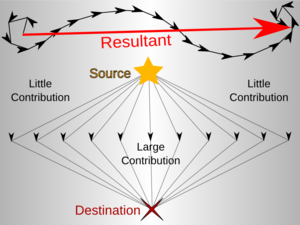
First, let’s show that photons actually travel in non-classical paths. In the setting below, light is emitted from the left and received by the small “black hole” on the right. There is a wall between them so the light can’t travel in the straight line. A mirror is placed at the bottom. You might think, the only way for the light to reach the “black hole” is to travel in the classical path shown below.

Now, if one removes the central and right part of the mirror, and also removes some parts on the left, as shown in the figure below, you would think that there is no light reaching the black hole. After all, the central part of the mirrow is where the light get reflected and reach the black hole.
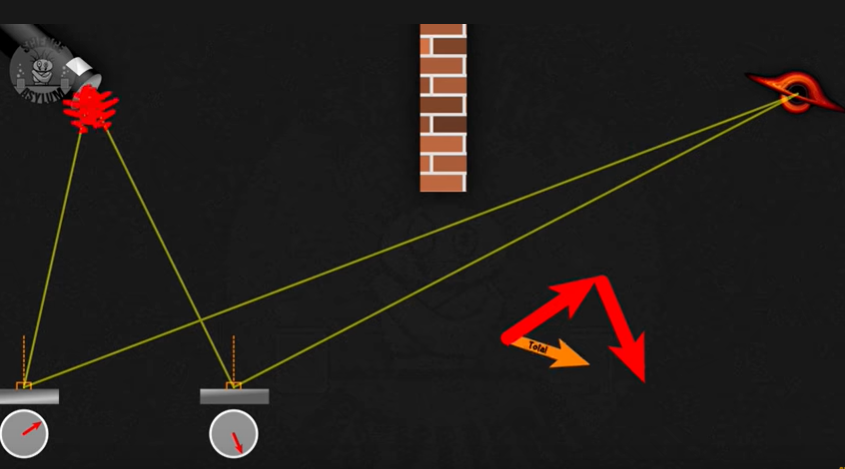
Contrary to what we believe, some light does reach the “black hole”! This demonstrates that the photons take all paths!
(The examples/figures above are from video by The Science Asylum. Another equally interesting video from the same channel is https://www.youtube.com/watch?v=cep6eECGtw4 )
Next, a natural question is, why we see the light travels in straight line? Why it is reflected by the mirror with equal incoming and reflecting angle?
We will have to understand that a photon has “phases”. The term “phase” is familiar to us when we study “waves”. In a nutshell, if two waves have aligned phases, when they come together they will form a bigger wave; if the phases are not aligned, then the final wave will be smaller or even disappears!

https://wiki.anton-paar.com/en/double-slit-experiment/
It turns out while the photons do take all the paths, only the “classical” paths are where the photons have aligned phases! To work this out, we really need to do some calculations. Here are the steps copied from https://en.wikibooks.org/wiki/A-level_Physics_(Advancing_Physics)/Quantum_Behaviour
- Define the light source.
- Work out the frequency of the photon.
- Define any objects which the light cannot pass through.
- Define the first point you wish to consider.
- Define a set of paths from the source to the point being considered, the more, the better.
- Work out the time taken to traverse one of the paths.
- Work out how many phasor rotations this corresponds to.
- Draw an arrow representing the final phasor arrow.
- Repeat steps 6-8 for each of the paths.
- Add all the phasor arrows together, tip-to-tail.
- Square the amplitude of this resultant phasor arrow to gain the intensity of the light at this point. It may help to imagine a square rotating around, instead of an arrow.
- Repeat steps 4-11 for every point you wish to consider. The more points you consider, the more accurate your probability distribution will be.
- Compare all the resultant intensities to gain a probability distribution which describes the probabilities of a photon arriving at one point to another. For example, if the intensity of light at one point is two times the intensity of light at another, then it is twice as likely that a photon will arrive at the first point than the second.
- If all the points being considered were on a screen, the intensities show you the relative brightnesses of light at each of the points.
I admit it’s not very easy calculations. But what matters is that we understand photons do take all the paths available, and when there are no photons, it’s only because the phases of the photons are misaligned.